下载app

原力研究 | 最全解读：1T算力，一年能获得多少FIL收益？

IPFS原力区

2020-08-18 17:21:01   阅读：10334

不进行研究的投资，就象打扑克从不看牌一样，必然失败！
本文由IPFS原力区Tony原作
不进行研究的投资，就象打扑克从不看牌一样，必然失败！
——麦哲伦基金的总经理彼得·林奇
本文会跳过推演过程，通过研究测试网2.0网络发展规律和预测未来网络发展的可能性，符合假定的情况下，直接给出直观的分析结论，具体要分析推演过程和概念可参考原力研究抵押系列文章《太空竞赛前，不得不读的干货》和《抵押多少FIL才能实现盈利？》。
上周推出《抵押多少FIL才能实现盈利？》文章后，因为该文章是假设在三个月满足基准供应1EB的全网算力，所以会有细心的读者提出反馈：假若网络延迟满足抵押收益会如何？对此，笔者针对计算了6个月、9个月和12个月全网算力达到1EB，解决算力延迟增长的收益问题，同时也寻求是否存在更高的收益可能性。
全网都暂时拟定FIL价格为100元、挖矿奖励为20天冻结期和180天的线性释放期，在基础算力为100PB、每日10PB增长、30天达到1EB后继续以7.5PB增长的全网增长模型中，该方式年利润为最高（184.83%）；假若早期全网算力增长过慢时，抵押成本过重、投资成本加重，后期算力的快速增长有利于早期奖励的释放，从而提高该算力的利润率。
一、回顾：90天（3个月）满足1EB全网基线供应，调小后期增长算力为7.5PB/日，年利润增涨17.46%
本次是拟定全网算力：基础算力100PB，每日增长10PB，90天达到1EB，同时结合测试网络2.0阶段在基线供应下的供应曲线，奖励爆块难度约是原本1PB基线标准的10倍，故回归得出90天内基线供应部分每天单个奖励数量约为
0.0115×T2+0.156×T+0.4281（T为天数）
通过《抵押多少FIL才能实现盈利？》文章可以略过推演过程，直接求出下面投资收益表。
每日10PB算力增长单T算力收益趋势表，来源：IPFS原力区，2020-08-10
从以上结果我们可以看出：

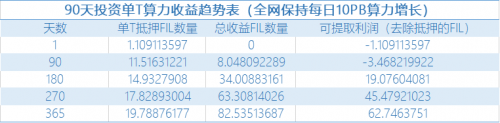
  • 假设投资者、基金会、425万FIL和开发团队每日线性释放，早期投资单T算力第一天需要质押成本大概1.1枚FIL；

  • 90天期间的盈收需要继续抵押，仍需要继续加注，累计折合共抵押3.4枚FIL；

  • 从90-180天阶段开始实现盈利，可提取利润大概19.1枚FIL，折合FIL单价为100元/枚，假设购买算力成本大概2000元，利润将近算力成本回本（管理费不同，暂时忽略，下同）；

  • 270天、365天利润核算，折合FIL单价为100元/枚，每T算力投资收益分别为93.79%和167.35%（以1T算力成本+3.4枚Fil抵押成本=2340元）。

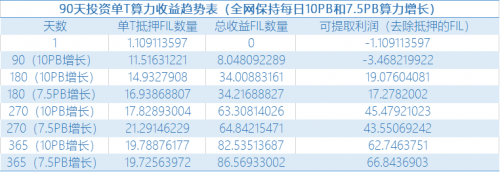
每日10PB和7.5PB算力增长单T算力收益趋势表，来源：IPFS原力区，2020-08-10
上次也提及到，之所以提出需要调整满足1EB后的增长方式，是考虑到持续每日10PB的算力增长是否符合单T收益最大化？所以笔者在结合满足第一年底满足3EB（200%增长基线供应需求），把后续的算力调到最小（每日增长7.5PB）来尝试，以上数据对比可以看出：

  • 第二、三个季度上，每日增加10PB和每日增加7.5PB的单T总收益差不多，只是后者抵押数量相对而言均摊抵押数量多了，导致前者可提取利润相对多一点；

  • 在第四个季度开始，每日增加7.5PB的单T收益上会逐步比每日增加10PB的高，主要是均分在每T奖励的数量多了；

  • 首年每日增加7.5PB收益为184.83%，较后者多17.46%收益，更为有利于早期参与者获益。可以预测：随着第二年开始，假如暂不考虑第三年的情况，持续每日增加7.5PB的单T总收益会比每日增加10PB的收益多。

那么接下来我们看看，假如6个月、9个月和12个月达到1EB全网算力会呈现如何的收益情况？
二、180天（6个月）：抵押过重的窘境与算力增长的分摊突围
抵押负重、收益削薄，年抵押成本增加跟不上总收益增加
同第3个月达到1EB设想一样，拟定全网算力：基础算力100PB，每日增长5PB，180天达到1EB，同时结合测试网络2.0阶段在基线供应下的供应曲线，奖励爆块难度约是原本1PB基线标准的40倍，故回归得出180天内基线供应部分每天单个奖励数量约为
0.0029×T2+0.039×T+0.107（T为天数）
直接求出下面投资收益表。
每日5PB算力增长单T算力收益趋势表，来源：IPFS原力区，2020-08-18
可以看出：

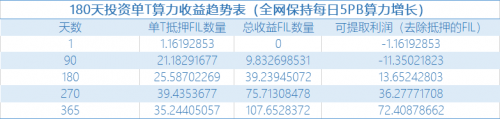
  • 早期抵押成本差距不大。早期投资单T算力第一天需要质押成本约1.2枚FIL，与90天达到1EB全网算力初始抵押差不多；

  • 前置抵押成本加重。90天期间的盈收需要继续抵押，仍需要继续加注，累计折合共抵押11.4枚FIL，比90天达到1EB假设多7.9枚FIL；

  • 抵押和收益同步增加，总收益增加5.6枚跟不上抵押成本增加7.9枚。其与90天达到1EB全网算力一样，都是在90-180天开始实现可提现盈利，并且抵押部分在逐步增加，年总收益较90天达到1EB假设增加约5.6枚FIL，跟不上抵押成本增加的7.9枚。

合理算力增长以扭转抵押过重，促进利润提升
每日5PB和11.5PB算力增长单T算力收益趋势表，来源：IPFS原力区，2020-08-18
为了检查是否有更好的方式实现单T的盈利最大化，同样带入了年底满足3EB的基线标准要求，所以引出了满足1EB全网算力后每日5PB和11.5PB的算力增长对比，如下：

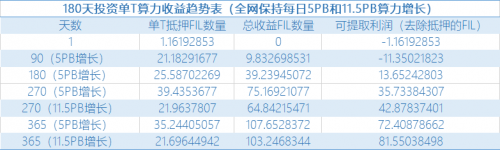
  • 第三季度抵押成本均摊导致利润差距局部增大。可以看到第三季度，每日11.5PB的算力增长利润开始超过每日5PB的算力增长，主要是因为算力的增长导致抵押成本减持；

  • 每日11.5PB首年可提取利润增长超过前者12.62%。可以看出，虽然每日11.5PB的算力增长总收益没有前者多，但是均摊的抵押成本降低了，所以净利润多9.1枚FIL，超12.62%；

  • 算力增长过慢会导致抵押成本负重。对于第三、四季度可以看出，算力的快速增长在一定程度上可以均摊抵押成本，转化可提现利润FIL，进而促进利润率增长。

三、270天（9个月）：基准供应的后期，扩展算力、均薄抵押、赎回利润
同上设想一样，拟定全网算力：基础算力100PB，每日增长3.5PB，270天达到1EB，同时结合测试网络2.0阶段在基线供应下的供应曲线，奖励爆块难度约是原本1PB基线标准的100倍，故回归得出270天内基线供应部分每天单个奖励数量约为
0.0012×T2+0.0156×T+0.0428（T为天数）
求出下面投资收益表。
每日3.5PB算力增长单T算力收益趋势表，来源：IPFS原力区，2020-08-18
可以得出：

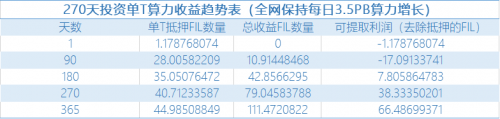
  • 90天抵押成本持续增加5.7枚。9个月达到1EB全网算力比6个月的抵押成本持续增加，因为算力增长过于缓慢，收益较少，导致每T算力抵押成本多承担5.7枚FIL；

  • 可提取Fil年收益较6月份达到1EB年降低8.9%。虽然后者年总收益111.5枚FIL比6个月的多，但是因为沉重过的抵押成本直接导致真正收益降少了5.9枚FIL，约8.9%。

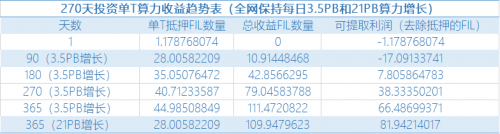
每日3.5PB和21PB算力增长单T算力收益趋势表，来源：IPFS原力区，2020-08-18

满足1EB基准供应需求后，以21PB（满足第二年3EB的基线供应）与3.5PB的每日算力增长对比：

  • 21PB算力增长分摊抵押，抢15.5枚FIL的利润。第四季度快速的算力增长有效释放抵押成本，转为利润。可以对比看出，21PB算力增长第365天抵押FIL比3.5PB提前释放了17.0枚FIL，虽然总Fil收益没有后者多，但是收益却多出了15.5枚FIL。

紧接着，我们猜测上线首先最坏的一种设想，在满足全网算力1EB的前提下，假若在最后一天达到1EB收益会如何？
四、365天（12个月）：抵押成“疾”，导致高收益、低可提取利润
拟定全网算力：基础算力100PB，每日增长2.6PB，365天达到1EB，同时结合测试网络2.0阶段在基线供应下的供应曲线，奖励爆块难度约是原本1PB基线标准的160倍，故回归得出365天内基线供应部分每天单个奖励数量约为：
0.0007×T2+0.0097×T+0.0268（T为天数）

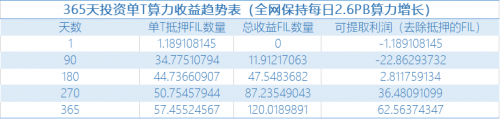
每日2.6PB算力增长单T算力收益趋势表，来源：IPFS原力区，2020-08-18

可以看出：

  • 90天抵押成本再次增加5.8枚。12个月达到1EB全网算力比9个月的抵押成本持续增加，因为算力增长过于缓慢，收益较少，导致每T算力抵押成本又多承担5.8枚FIL；

  • 总收益高，抵押高，可提取利润较低。第365天，虽然每日2.6PB算力增长的总收益比每日增加10PB多（90天达1EB）37枚FIL，因为其总的抵押成本也多负重了37枚FIL抵押，实际可提取利润几乎无增长；

  • 算力增长过慢，抵押负重成疾，其中第270天有超过50%的收益占据抵押。

五、年利润博弈：90日天达1EB、后调7.5PB/日算力增长以184.83%荣获高利润榜首

90天、180天、270天和365天达到基准供应标准以及不同调配的年收益率对比图，来源：IPFS原力区，2020-08-18
从上，我们可以得知：

  • 184.83%为最高年利润。90日天达1EB、后来每日7.5PB算力增长的年利润最高为184.83%，单T抵押数量最少约为19.73枚FIL，即是成本也是最少；

  • 缓慢的算力增长会导致投资成本和风险提高同时也降低收益。虽然每日以2.6PB算力增长、第365天达到1EB方式中FIL总收益是最高，但是因为其全网算力增长过慢，导致单T抵押的成本过高，直接导致实际可提取的FIL较少，以及抵押大量的FIL会导致支出成本、风险过高；

  • 算力增长时缓解抵押负重和提高收益的解决方式。“180天达1EB，后11.5PB增长”和“270天达1EB，后21PB增长”皆是调整后的算力增长，年利润率都近160%，假如两者对于算力不做调整可以看出，算力增长过慢，导致算力抵押成本过重，可提取利润降低；后期算力增长快速增长，可以快速分担抵押的成本，释放抵押的利润；

  • FIL价格的不确定性为加注抵押成本提高了风险。通过全网算力缓慢增长以满足1EB的全网算力的对比可知，算力增长越慢，抵押成本越高，假如FIL价格变化过大会导致后期收益有可能得不偿失；同时收益率也逐步下降。

总而言之，我们很难在实际情况中循序概念中的发展路径，当全网算力增长越慢，越有可能继续加重抵押成本，年利润降低，后期快速增长可以有效释放抵押成本，实现利润提取；当增长过快的时候，降低增长速度，匹配第二年基准供应标准即可，提高单T算力的收益。
根据笔者观察，在达到算力满足基线供应标准时的供应量时是最大，在该时间段前后投资算力的奖励较高，但是也伴随着当时行情单价不同而导致成本不同，风险也会随之提高，还有一系列积累的有效算力等等问题。
PS：本文仅作研究分析，不做投资建议，望读者谨慎投资；若本文数据与前文不同，以本文为主，因本文推演方法与前文皆为一致，数据和算法更为精确、优化。
／End.

声明：本文系IPFS原力区原创稿件，版权属IPFS原力区所有，未经授权不得转载，违者将依法追究责任。
提示：投资有风险，入市须谨慎。本文不作为投资理财的建议。

声明：此文出于传递更多信息之目的，并不意味着赞同其观点或证实其描述。本网站所提供的信息，只供参考之用。

点击阅读全文