原力研究 | Filecoin主网攻略:算力增长越快,收益越高?
兵无常势,水无常形,能因敌变化而取胜者,谓之神。
——孙子
最近太空竞赛有一个特征:变;同时投资者和矿商也随机应变,投资者应变调整投资配比,矿商应变调整运维和硬件、拓展运维技术输出。
本篇根据截至9月8日官方最新提出的经济模型调整以及目前太空竞赛算力的增长情况来进行年收益推演。这次主要针对抵押系列四篇文章推理过程,结合太空竞赛的最新情况来进行分析,若有推演细节不理解,请按顺序回顾以下文章:
《太空竞赛前,不得不读的干货》
《抵押多少FIL才能实现盈利?》
《最全解读:1T算力,一年能获得多少FIL收益?》
《缔造Filecoin经济》
《解读:首日单T抵押34.76枚》
本文主要结论是:在后置未完全释放完毕、部分不作为前置抵押初始资金的情况下,每日10PB、20PB算力增长年收益分别为65.08%和49.72%;在后置未完全释放完毕、部分作为前置抵押初始资金的情况下,每日10PB、20PB算力增长年收益分别为135.29%和67.83%。同时笔者也提议全网可以在早期共同提高算力适当增长以应对高抵押成本的风险和缩短币价波动的周期。
一、模型的调整以及前提基础数据
本次经济模型做出的最新调整如下:
取消20天冻结期,直接开始180天的线性释放;
后置未完全释放完毕部分作为前置抵押初始资金暂未确定,代码层面未作修改;
扇区提前终结费上限为70天或者扇区服务时间的一半,两个取小值;
交易抵押部分由5%调整为1%;
扇区错误检测费由开始的5天收益调整为3.5天收益;
初始基线标准调整为2.5057116798121726EB,每天以100%增速提高,即是第一年底基准会达到5EB,第二年底10EB。
取消冻结期20天,收益部分直接后置180天线性释放,该行为将直接有利于矿工收益的提前释放;
每个高度幸运爆票数修正为3.82616233973628倍。上次截止10242高度之前的规律,得出平均每个高度会有4.23911741214058倍数的爆块数(包含节点和幸运票数),该次截止到43834高度,得出平均每个高度会有3.82616233973628倍数的爆块数,数据量大更为趋势实际情况;
30%流通抵押减去前20天预期收益每日支出累计的抵押数量。真实FIL流通量=投资者、基金会和开发团队释放+挖矿释放-前20天预期收益的总抵押;
太空竞赛预计第一阶段计释放为265万枚FIL。目前最新情况预测,全球奖励估计会包含全球奖励150万+亚洲50万+欧洲、北美洲、大洋洲10万+全球10万爆块排名奖励+25万BUG奖励,总计265万FIL奖励,与官方计划的485万枚FIL相比少了将近一半;

图1,根据拟定调整大概每天释放33.4357枚FIL,来源:IPFS原力区,2020-09-09
根据采集样本以及根据新基准情况模拟调整完善基线供应规律。笔者会根据增加高度的样本来拟定在首年以2.5EB满足到5EB的基线供应标准情况,并以43834高度为的基线供应规律为论证基础(上次截止10242高度),模拟求出基线的供应规律。
基本要素了解完后,接下来我们聊聊假如按照目前太空竞赛的算力增长(10PB/day)情况作为主网上线,矿工的收益如何?20PB、30PB呢?
二、10PB、20PB OR 30PB,算力增长越快年收益率越高?
1)每日10PB增长:单T年收益47.94%/72.10%(前置未释放做启动抵押收益)
本段会根据每日10PB增长作为主网上线情况进行假设,以及把后置抵押部分作为初始抵押资金作为一个对比条件,并代入上段提出的调整数据进行运算,得出以下第90天、180天、270天及365天的收益对比,得出下图。

图2,单T每日增长10PB年收益对比,来源:IPFS原力区,2020-09-10
由上图可以看出:
第一天抵押数量为29.3330655772007枚FIL,与上篇有些差异是因为每个高度幸运爆票数、基线供应根据更多的数据、初始基准和增长率变化规律做出修正;
随着时间增加,单T抵押FIL数量(包含预期20天收益抵押+30%流通抵押)增多,虽然预期20天收益抵押部分是减少的,但是主要是30%的流动抵押逐渐增加;
前置未释放做启动抵押,收益可增24.16%。从结果上看,后置抵押作为前置抵押的启动资金,年收益比前者多将近10枚FIL,同时因为前者需要付出的成本(假设:2000元1T+1FIL/100元)较多导致可提现FIL多了,所以后者年收益多出24.16%;
10PB日增长供应公式。因为主网上线基线标准设定变了,所以根据笔者拟定主网基线供应情况为太空竞赛的1/2.5倍数较为适合,综合得出在全网算力达到5EB前每日供应量供应为{330000000×EXP(-1.09897764548444E-07×((T×2880+1)-1))×(1.09897764548444E-07)/5)+(0.0634×T -0.0164)}×3.82616233973628×2880(T为天数)。
2)每日20PB增长:年收益63.41%/86.92%(前置未释放做启动抵押收益)
拟定每日20PB算力增长,得出第90天、180天、270天及365天的收益对比下图。

IPFS原力区可以得出结论:
首日抵押7.68568111796023枚FIL。因为初始基线值较大和早期算力较少,20PB日增长不会让爆块数量增长很明显。同时早期30%流动抵押很小(早期算力少、流通盘少),预期20天收益抵押由更多算力进而均摊,故单T抵押会大大减少;
抵押收益和增长缓慢。可以看出单T抵押和收益总数增速逐步减慢,主要是后期越来越多的算力参与均分;
前置未释放做启动抵押,收益可增24.51%。因为更多算力的参与,在一定程度上可分摊抵押成本,分摊的比收益的明显,故总收益比每日10PB增长的收益高。同时在是否采取后置抵押作为前置抵押资金前后者的收益差距为24.51%;
20PB日增长供应公式。因为结合主网上线基线标准设定调整,所以根据笔者拟定主网基线供应情况为太空竞赛的1/1.9倍数较为适合,综合得出在全网算力达到5EB前每日供应量供应为{330000000×EXP(-1.09897764548444E-07×((T×2880+1)-1))×(1.09897764548444E-07)/5)+(0.0834×T -0.0216)}×3.82616233973628×2880(T为天数)。
3)每日30PB增长:年收益68.72%/89.43%(前置未释放做启动抵押收益)
同样拟定每日30PB算力增长,得出第90天、180天、270天及365天的收益对比下图。

图4,单T每日增长30PB年收益对比,来源:IPFS原力区,2020-09-10
IPFS原力区结论如下:
首日抵押3.3048196382271枚FIL。因为算力的增速增快,抵押逐渐减少;
比10PB、20PB提前三个月开始收益与抵押收支平衡。对比可以看出前两者都是在第六个月开始实现提现FIL,而日增长为30PB在第三个月可实现提现,不用继续加注抵押成本;
前置未释放做启动抵押,收益可增20.71%;
30PB日增长供应公式。因为结合主网上线基线标准设定调整,所以根据笔者拟定主网基线供应情况为太空竞赛的1/1.2倍数较为适合,综合得出在全网算力达到5EB前每日供应量供应为{330000000×EXP(-1.09897764548444E-07×((T×2880+1)-1))×(1.09897764548444E-07)/5)+(0.1321×T -0.0342)}×3.82616233973628×2880(T为天数)。
4)三者对比:算力增长越快,收益越高,风险越低
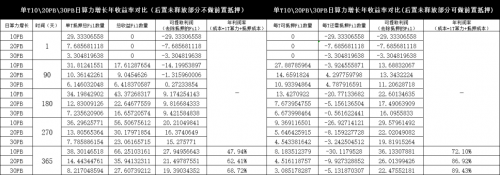
图5,每日10PB/20PB/30PB算力增长年收益图对比图,来源:IPFS原力区,2020-09-10
通过上图可以看出:
随着算力增速增长,抵押负担轻,年收益。因为对于早期而言,爆块收益增长不大的情况下,更多的算力增长有利于抵押风险的分担。同时年收益也在逐步增长,分别为47%/72.10%(10PB)、62.41%/86.92%(20PB)和68.72%/89.43%(30PB);
后置抵押做初始启动抵押资金,收益更高,更会缓解早期FIL流通不足、矿工抵押成本。后置抵押做前置抵押资金日更有利于矿工收益,但随着收益越来越少,前后者差距逐渐在减少,差距分别为24.16%(10PB)、24.51%(20PB)和20.71%(20PB)。不过笔者预测,随着算力逐步增加,抵押收益会逐渐减少,两者差距会逐步减少,不过该政策在一定程度上可以缓解早期的矿工抵押压力;
后置抵押做启动资金能缩短收益周期。若定下使用,则基本可以在3个月内实现提现,否则需要延迟至6个月内;
在10-30PB区间,增速越快、抵押越少、收益越高。虽然10PB日增长的年总收益是最高为66.24枚FIL,但是因为其抵押过高,在一定程度上可提现的FIL较少。反而30PB的年总收益为27.61枚FIL,支出抵押成本低,收益确实最高。
对此,归根到底还是要取决于全网算力增长的快慢来取决于早期抵押成本、回本周期以及收益率。
三、应对主网上线的猜想:早期算力增长较快可能是一种妥当的方式
基于早期抵押成本会过重的考虑,对于矿商而言,IPFS原力区认为可能会采取两种方式:早前算力增长过慢或者早期算力增长过快。
早前算力增长过慢:基准网络延迟解决
早期增长过慢不一定有利于早期矿工。全网算力假如增长过慢,假设基线供应将近0,前期20天预期收益主要体现为简单供应爆块。同时因为算力减少了,在一定程度上爆块概率以及单个高度票数可能会减低,收益会降低,抵押也会随之减少。但算力少到一定程度,简单供应又在一个高爆块概率和单个高度票数情况下,收益可能会较高;
后进入矿工可能存在一定高预期收益抵押支出。等在算力慢慢进来,待算力增长到一定程度,收益提升后,后者在某个高收益时间段进入的算力需要付出较高的前期抵押(主要是针对20天预期收益的抵押),同时对于最早期进来参与的矿工获益是:算力抵押低以及有效算力最大化的积累;
可能导致延迟满足基准网络需求。但该做法同时也存在会延迟满足基准网络的标准以及市场上流通盘(投资者、基金会和开放团队的释放)的增加,导致30%流通抵押成本加重的同时也会间接导致第二年难以跟上的连锁反应,爆块获得的奖励难以恢复正常衰退标准。
早期算力增长过快:利大于弊
合理增长是可以实现收益分摊大于抵押分摊,逐步提高年收益。全网算力假如过快,在一定程度上可以分摊抵押、风险,抵御币价波动的风险的同时也可以满足基线网络要求。假如增长合理的话可能会实现首年的年收益最大化,主要原因是均摊收益大于均摊抵押,例如上章论证30PB日会提前三个月实现实现提现以及年收益也比10PB、20PB高;
算力增长极快也很有可能会在首年实现不盈利情况。假设一定极端情况,第一天全网达到3EB及整年保持在一个3EB的水平(不太现实的设想),同时考虑180天线性释放的前提下,单T年总收益约为29枚FIL,同时考虑早期算力成本(2000元)、流通盘(投资者、基金会和开放团队的释放)过大、还需要早期支出过重的30%流动抵押成本、后期收益较慢获和价格波动的情况下,很有可能难以实现盈利。
综合而言,笔者认为算力增长较快是一种较为可选择的方法,一来需要面对投资者、基金会和开放团队的释放,时间越长,流通越大,该部分的抵押成本越大,不适应算力拉长战线增长;二来,算力增长过快可以说明全网矿商都具备较为成熟的运维水平,可以根据全网情况来进行调配算力增长,降低投资风险的同时也保证稳定的收益,以实现早期参与的矿工获得收益,以促进后面投资者的介入,更为良性地促进存储和检索市场逐步壮大。
PS:因数据样本有限、建立模型与设定标准有差异以及太空竞赛环境不一定满足主网上线的真实情况,故文中提及关于在满足基准线前的供应规律以及基准网络标准增长规律会与官方提及或者实际情况存在一定的出入。本文仅作研究分析,不做投资建议,望各位投资者谨慎投资。

声明:本文系IPFS原力区原创稿件,版权属IPFS原力区所有,未经授权不得转载,违者将依法追究责任。
提示:投资有风险,入市须谨慎。本文不作为投资理财的建议。
声明:此文出于传递更多信息之目的,并不意味着赞同其观点或证实其描述。本网站所提供的信息,只供参考之用。








