在之前的一篇文章中，我介绍了Merklix树(（译者注：Merklix 树和Merkle树的解释可以查阅原文作者的另一篇博文《Introducing Merklix tree as an unordered Merkle tree on steroid》)作为一种加密方法来描述无序集或无序图。这可以证明一个元素包含或者不存在于 o(ln(n))的数据结构中，并使用这些证明来改变结构，即使不知道它的全部内容。
我现在将解释如何使用它来帮助处理像比特币这样的区块链技术中的UTXO集。
在进入UTXO部分之前，让我们演示如何使用一个Merklix树来证明集合中元素的存在或不存在。
在这个例子中，我们试图证明Item1是在集合中的。我们通过提供Item1或其散列，6eec，来说明，由于我们不想显示Item1或只是希望使证明更简洁，它们在图中用红色标示。
然后我们在树中提供一个通向根的路径。此路径在图中用黄色标示。要验证证明，一个散列6eec与3738得到bf1b，它自己散列与d9fe得到2812，树的根。我们证明了元素确实在树中。
现在让我们假设我们想证明Item5不在树中。 它的散列是cd5a，其中c = 1100。
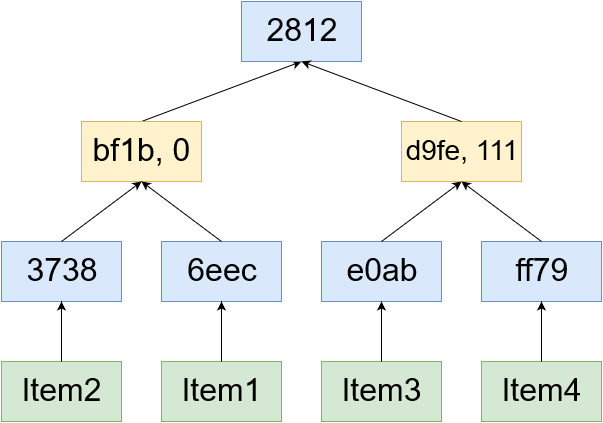
相同的，证明是由黄色的元素得到。通过将bf1b和d9fe一起进行散列，可以验证它们都是树的一部分，并且它们是同层级。 bf1b作为从0开始的所有元素作为其子项，d9fe是从111开始的元素。因此，Item5不可能是这些子树中的任何一个。然而，如果它在树中，它将在这两个节点之间。因为这两个节点是同层级，我们都知道两者之间没有什么，因此可以断定Item5不在该集合中。
因为树中的路径是证明提供的，所以它也可以用于修改树本身。再次说明，这项工作并不需要通往根节点路径的先验知识（译者注：这句话我不能保证译的准确，原文是：this work without prior knowledge of the tree past its root.）。现在我们证明了Item5 不在树中，但也许我们想添加它呢？
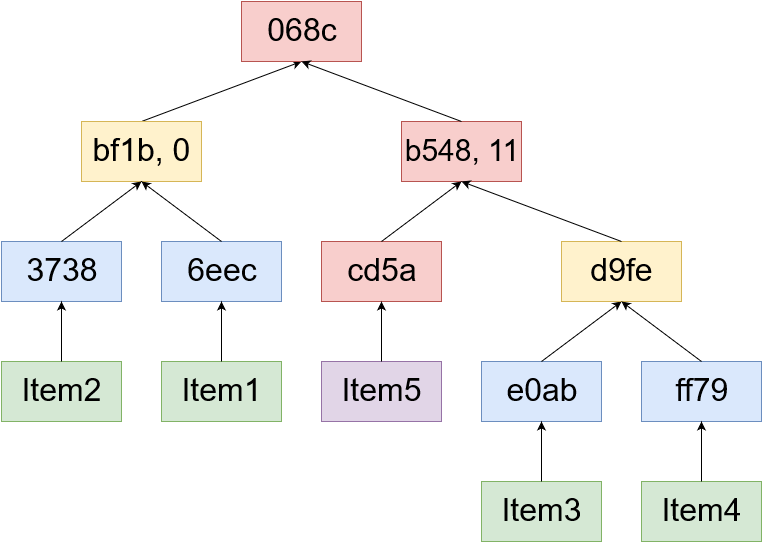
树中的新节点用红色表示。图中黄色部分表示的是证明中的区块。正如你所看到的，一旦插入Item5 ，树的根节点可以仅使用证明中散列们来计算。
我们还有一个证明，Item1是在集合中，让我们删除它。
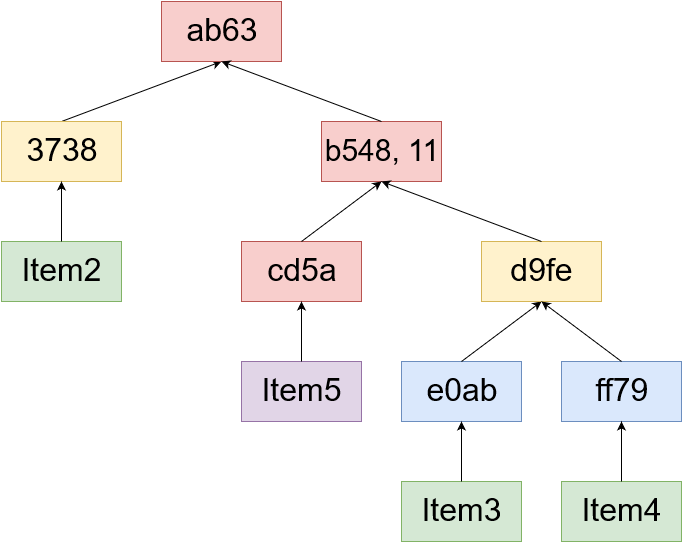
再一次，需要计算删除结果的唯一散列要么包含在证明中，要么在插入Item5时被计算。
从这一点，我们可以得出结论：：如果k << n，我们可以在o（k * ln（n））中的n个元素的Merklix树中保持一组k个变化，并且当k变大时，趋向于o（k）。变化集在图中用红色表示。
可以通过使用txid 作为关键（译者注：这里的“关键”原文是“key”，我不太确认这样译是否很好）和一些未使用输出的序列化的作为值在 Merklix tree 表示UTXO集。为了简单说明，在上面的插图中，我一直使用散列的值作为关键（key），但是没有这样的义务。我不会继续深入到未使用的输出如何被序列化，知道这些已经足以了解这个概念。
当通过网络发送交易的时候，也有可能发送一个在UTXO 集输入的证明。这将允许接受交易和证明的节点避免查询它们的UTXO 集， 这可能是一个缓慢的过程，特别是如果集很大并且需要在磁盘上。
此外，这使节点可以修剪UTXO集的一部分。他们可以使用存在的证明来更新他们的UTXO集，包括修剪的部分。假使一个交易没有证明，可以向没有修剪的UTXO 集的该部分的另一节点请求证明。如果证明显示输入在UTXO集中，那么可以在其他方面进行检验，并且如果这是有效的，交易可以转发到其他节点。如果证明显示不存在，则交易因无效而被拒绝。
一般认为，网络上的节点不应相互信任。在不能构成证明的情况下，这将不是问题。节点不能说谎。更糟的是，节点可以拒绝回答，在这种情况下，请求可以被转发到另一个节点。
因此，实际上只有非常少的节点需要查询它们的UTXO 集，并且工作量可以分布在许多节点上。这将是比特币区块链中横向扩展（horizontal scaling）的第一个例子。通过这样的措施，UTXO 集可以通过只用一个节点的子集来处理每个它的每个分片就可以疯狂地增长到很大的规模。子集中的节点负责它自己请求分片的子集。
例如，使用大约5000个节点，可以分割UTXO 64路，每个分片大约有78个节点。
即使我们认为这些节点的一半不可信，并且不会回答请求，每个分片留下39个节点。
它可以有效地将每个节点的存储需求减少64个，其UTXO检查工作量减少2500个。在绝对数量上，一个1.5Gb的UTXO 集，一个节点需要大约24Mb的内存，一个区块只需要检验一小部分的UTXO，网络就可以处理当前的工作量。
如果节点采用智能策略，例如保持记忆高速的货币周转率（译者注：暂时未能理解这句的意义，原文是：such as keeping in memory high velocity money and committing to disk and pruning from memory asynchronously savings,），提交磁盘并从不同步的记忆保存中裁剪，网络作为一个整体可以实现极高吞吐量的UTXO请求，例如没有形成一个显著的问题下，允许UTXO 集几个数量级的增长。
虽然节点可以通过遍历整个区块链的历史来重构UTXO 集，但是这个意味着一个新节点的自我启动时间是 o(n*t)，其中n是交易量和t 时间。这只会随着时间变得越来越糟糕。如果节点可以获得根散列的UTXO 集，那么节点就可以快速变得有效。
这可以通过将它放到coinbase 交易中作为软分叉来实现，但是最好将它放到区块头部中作为硬分叉来实现。这样，一个节点只要连接了就可以在网络上开始验证，并反向对已知有效区块开始验证以及作为网络进程转发。
声明：此文出于传递更多信息之目的，并不意味着赞同其观点或证实其描述。本网站所提供的信息，只供参考之用。
